Las bases de numeración o cómo hacer trucos de magia binarios
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Las bases de numeración o cómo hacer trucos de magia binarios MATEMOCIÓN
En la anterior entrada del Cuaderno de Cultura Científica titulada El arte de la sencilla baldosa de Truchet hablábamos de la expresión del número pi en base cuatro, en la que utilizamos las cuatro cifras básicas 1, 2, 3, 0, y dejamos para una entrada futura, que es la que hoy tenéis delante, explicar las diferentes bases de numeración y cómo obtener las expresiones de cada número en dichas bases.

Para empezar, recordemos que el sistema de numeración posicional moderno utilizado en casi todo el mundo es decimal, es decir, que tiene base 10 (véase el libro Los secretos de la multiplicación, de los babilonios a los ordenadores). Por lo tanto, consta de diez cifras básicas, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y todo número se puede representar con ellas al expresarlo en función de las potencias de 10. Por ejemplo, el número 3.457 tiene el valor de 3 veces la cantidad de 1.000, 4 veces la cantidad de 100, 5 veces la cantidad de 10 y 7 veces la unidad 1, que son las potencias de 10, a saber, 1.000 = 103, 100 = 102, 10 = 101 y 1 = 100.
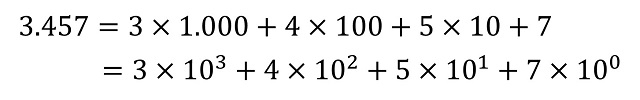
En general, dada una base de numeración b –ya sea esta igual a 2, 3, 12 o 60- la representación posicional de cualquier número en la misma viene dada por una expresión d1d2…dr (donde los dígitos di –para i entre 1 y r– pertenecen a la familia de las b cifras básicas del sistema de numeración, que tienen valores entre 0 y b – 1) teniendo en cuenta que el número puede escribirse, de forma única, como
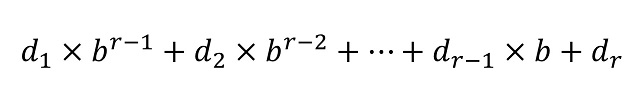
Por lo tanto, la representación del número está ligada a la base elegida. Así, si tomamos el sistema binario (b = 2) el anterior número se representa como (110110000001)2, ya que “3.457” = 211 + 210 + 28 + 27 + 1; en la base octal (b = 8) como (6600)8, porque “3.457” = 6 x 83 + 6 x 82; o en la base hexadecimal (b = 16), donde las cifras básicas son 0, 1, …, 9, A, B, C, D, como (D81)16, puesto que “3.457” = D x 162 + 8 x 16 + 1, donde estamos utilizando el subíndice de las representaciones (2, 8 y 16) para recordar que esa es una representación en esa base de numeración.
La base de numeración binaria
Veamos esto más despacio para el caso de la base binaria, b = 2. En este caso solamente hay dos cifras básicas, 0 y 1, y expresar un número N en el sistema binario es escribirlo como suma de potencias de 2, donde cada dígito nos dice cuántas veces se toma esa potencia (como las cifras básicas son solo 0 y 1, entonces cada dígito nos dice si está o no dicha potencia). Así, si tenemos una expresión binaria como (101101)2, podemos saber cuál es su valor viendo qué potencias de 2 nos indica esa expresión que aparecen. Como el número binario tiene 6 dígitos, eso quiere decir que las potencias implicadas son 25 = 32, 24 = 16, 23 = 8, 22 = 4, 21 = 2 y 20 = 1 y los dígitos nos dicen si la correspondiente potencia está o no, como se muestra a continuación,

entonces, el número expresado con la representación binaria (101101)2 es 1 x 32 + 0 x 16 + 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = 32 + 8 + 4 + 1 = 45.
De hecho, este es el método general para pasar de un número binario a su expresión decimal, que es la que nosotros entendemos mejor. Esto es, se cuentan cuántos dígitos r hay implicados –por ejemplo, en la expresión binaria 1110100001011001 hay 16 dígitos- y se van considerando qué potencias de 2, desde 2r-1 hasta 20 = 1, aparecen en función de si hay un 1 o un cero en la correspondiente posición, empezando por la derecha (aunque también podríamos realizar esa lectura empezando por la izquierda y tomando las potencias desde 20 = 1 hasta 2r-1) –por ejemplo, en la expresión binaria anterior, 1110100001011001, aparecen las potencias 215 = 32.768, 214 = 16.384, 213 = 8.192, 211 = 2.048, 26 = 64, 24 = 16, 23 = 8 y 20 = 1, por lo tanto, el número representado en forma binaria por (1110100001011001)2 es el número representado en el sistema decimal como 59.481.

Recíprocamente, si queremos ver cuál es la representación binaria de un número N, por ejemplo, el número N = 197, tendremos que ver cómo expresarlo como suma de potencias de 2. Como las potencias de 2 que pueden verse implicadas son 27 = 128, 26 = 64, 25 = 32, 24 = 16, 23 = 8, 22 = 4, 21 = 2 y 20 = 1, ya que 28 = 256 ya es mayor que el número en cuestión, tenemos que ver cómo expresar el número 197 como suma de estas. Para empezar, en nuestra expresión aparecerá 27 = 128, además, 197 – 128 = 69; por lo tanto, también aparecerá 26 = 64; como 69 – 64 = 5, no aparecerán 25 = 32, 24 = 16, ni 23 = 8, pero sí 22 = 4; por último, 5 – 4 = 1, que es 20. En conclusión, 197 = 128 + 64 + 4 + 1 y la expresión binaria es (11000101)2.
Podemos dar un algoritmo general teniendo en cuenta el conocido como teorema de la división o lema de la división de Euclides, que nos dice que si tenemos un número natural a (dividendo), que queremos dividirlo por un número natural b (divisor), nos dará como resultado un cierto número natural c (cociente) y nos quedará de resto un número r, que toma valores entre 0 y b – 1, que ya no se puede dividir por b, de manera que podemos expresar la división como a = b x c + r. El lema de la división de Euclides es el que nos permite afirmar que todo número N puede expresarse, de forma única, como suma múltiplos de potencias de la base, es decir, como
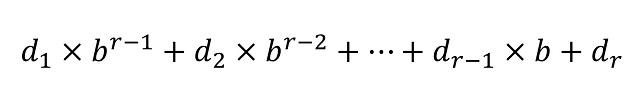
La idea del algoritmo de cambio de base está en utilizar, hasta que ya no podemos hacerlo más, el teorema de la división. Dado un número N que queremos cambiar de la base decimal a la base b se aplica el lema, primero considerando N como dividendo y después, en cada paso, el dividendo será el cociente del paso anterior. Veámoslo con un ejemplo concreto, por ejemplo, el número anterior N = 197.
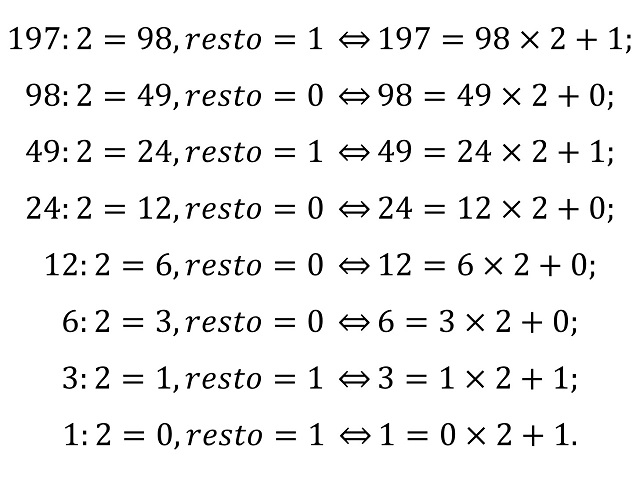
De forma que, si tomamos las raíces y las colocamos de izquierda a derecha, es decir, empezando por las unidades, obtenemos la expresión binaria del número, en este caso, de 197, así: 11000101, como ya habíamos visto antes.
Esto se debe a que, de nuevo en este ejemplo, aunque es algo general, aplicando el teorema de la división se obtiene
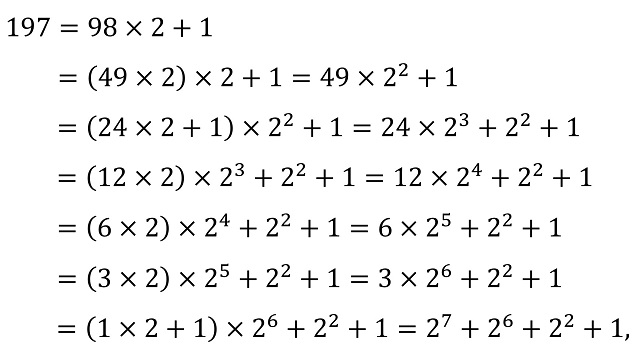
es decir, la expresión de N en las potencias de 2.

Un truco de magia binario
Existe un sencillo truco de magia relacionado con los números binarios. Es muy sencillo y podéis hacérselo a vuestros familiares y amistades. Es un truco relativamente conocido, que incluso alguna empresa ha utilizado para su publicidad, como el siguiente ejemplo “Estas cartas son mágicas” de la empresa Coca Cola.


Expliquemos en qué consiste el truco de magia de las tarjetas numéricas. Se le pide a una persona que piense en un número del 1 al 63. Aunque también se puede complicar esto un poco y hacer un poco de espectáculo, es decir, podemos inventarnos cualquier acción para que alguien del público acabe obteniendo un número del 1 al 63, pero que nosotros debemos desconocer.
Una vez que esa persona del público tiene en la cabeza el número, entre 1 y 63, determinado, que nadie más conoce, se le muestran las siguientes seis tarjetas y se le pide que nos diga en cuál de ellas está el número que ha elegido. Le vamos preguntando “¿está en esta tarjeta?” y nos irá contestando “sí” o “no”. Si contesta “sí” sumamos el número de la esquina de la tarjeta correspondiente y si contesta “no” no lo sumamos. Al para todas las tarjetas el resultado final de la suma será el número que esa persona tiene en la cabeza. Las tarjetas son las siguientes:






Por ejemplo, imaginemos que una persona nos contesta lo siguiente al mostrarle las tarjetas: sí, sí, no, sí, no y sí, entonces el número que ha pensado es 1 + 2 + 8 + 32 = 43.
¿Cuál es la base de este truco? Como podemos imaginar la base es el sistema binario de numeración, como vamos a explicar brevemente. Empezando por el final, cuando la persona del público nos va diciendo en cada tarjeta si el número está –dice “sí”- o no está –dice “no”-, realmente nos está dando la representación binaria del número que ha pensado. Por ejemplo, en el caso anterior (sí, sí, no, sí, no y sí), sería (1 0 1 0 1 1)2 –ya que las hemos mostrado desde las unidades- que no es otro que 25 + 23 + 2 + 1 = 43.
Esto es así porque a la hora de crear las tarjetas, en la primera tarjeta, la que tiene un 1 en la esquina, están todos los números que tienen un 1 en la primera posición de la derecha de su representación binaria, que son todos los impares. Podemos comprobarlo en la siguiente lista con las representaciones binarias de los números entre 1 y 63.
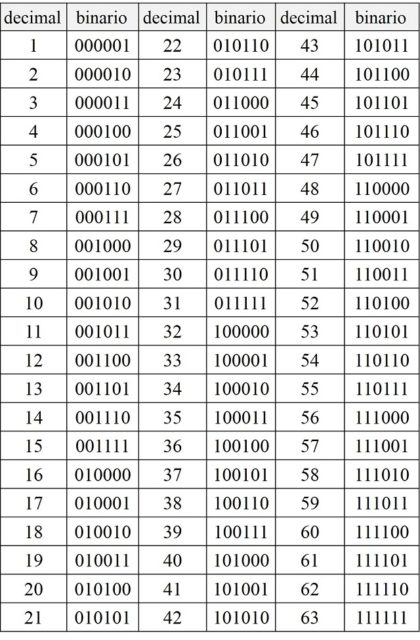
En la segunda tarjeta están los números que tienen un 1 en la segunda posición de la derecha de su representación binaria (2, 3, 6, 7, 10, 11, 14, 15, …, 62, 63), en la tercera los que tienen un 1 en la tercera posición de la derecha de su representación binaria (4, 5, 6, 7, 12, 13, 14, 15, …, 60, 61, 62, 63) y así hasta la última tarjeta.

La base duodecimal
A lo largo de esta entrada hemos hecho hincapié en el cambio de base del sistema binario, pero todo lo comentado sirve para cualquier otra base, ya sea la base 12 (del sistema duodecimal, del que hablamos algo en la entrada El sistema duodecimal, o si los humanos hubiésemos tenido seis dedos en las manos), la base 60 (que utilizaban los babilonios y del que hablamos algo en la entrada ¿Sueñan los babilonios con multiplicaciones eléctricas?) o cualquier otra base.
Terminemos con un ejemplo para la base 12, la duodecimal. Denotaremos las cifras básicas de este sistema de numeración como 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B (donde A tiene el valor de 10 y B de 11). Consideremos en número 13.762 y expresémosle en base 12. Si consideramos el algoritmo de la división de Euclides, tenemos que:
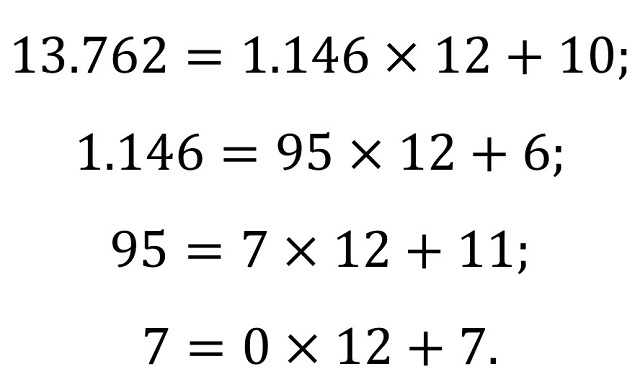
Por lo tanto, los restos son 10, 6, 11 y 7, que, si recordamos que el primero corresponde a las unidades (parte derecha de la representación duodecimal), nos da la representación del número 13.762 en base 12 como
![]()
La siguiente cuestión será cómo representar los números que no son naturales (ni enteros), como 0,25; 3,7675 o el número pi, pero de eso hablaremos en la siguiente entrada del Cuaderno de Cultura Científica.
Bibliografía:
1.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Catarata, 2019.
2.- George Gheverghese Joseph, La cresta del pavo real, las matemáticas y sus raíces no europeas, Pirámide, 1996.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
.jpg)
.jpg)
.jpg)